bits bytes and integer 2
无符号数加法
由于正数的补码和原码一样,下面所提到的 bit 既可以认为是补码,也可以认为是原码。
因为任何计算机用来存储 bit 的设备都是有限的,所以如果所需的用来存储两个数之和的 bit 位超出了硬件设备的 bit 位,最高位则会被丢弃。
假设有 bit 位 4 位,则能表示的所有状态为:
0000000100100011010001010110011110001001101010111100110111101111
可以这些状态来分别代表 0-15 着 16 个数字。
不溢出
| bit | 值 | |
|---|---|---|
| 加数 1 | 0001 | 1 |
| 加数 2 | 0001 | 1 |
| 和 (不忽略进位) | 0010 | 2 |
| 和 (忽略进位) | 0010 | 2 |
结论:期望值是 2,最后的结果是 2
溢出
这个章节,视频和课件对不上,课件在第 35 页,但是课程一开头就讲这个章节

两个无符号数相加,如果最高位溢出了,会被丢弃。相当于真正的结果对 w 取模。
| bit | 值 | |
|---|---|---|
| 加数 1 | 1101 | 13 |
| 加数 2 | 0101 | 5 |
| 和 (不忽略进位) | 10010 | 18 |
| 和 (忽略进位) | 0010 | 2 |
结论:期望值是 18,最后的结果是 2,相当于 18 对 16 取模
可视化(数学)整数加法

从上图可以看出:
- 两个数的取值范围是 0 - 15
- 两数之和的取值范围是 0 - 30
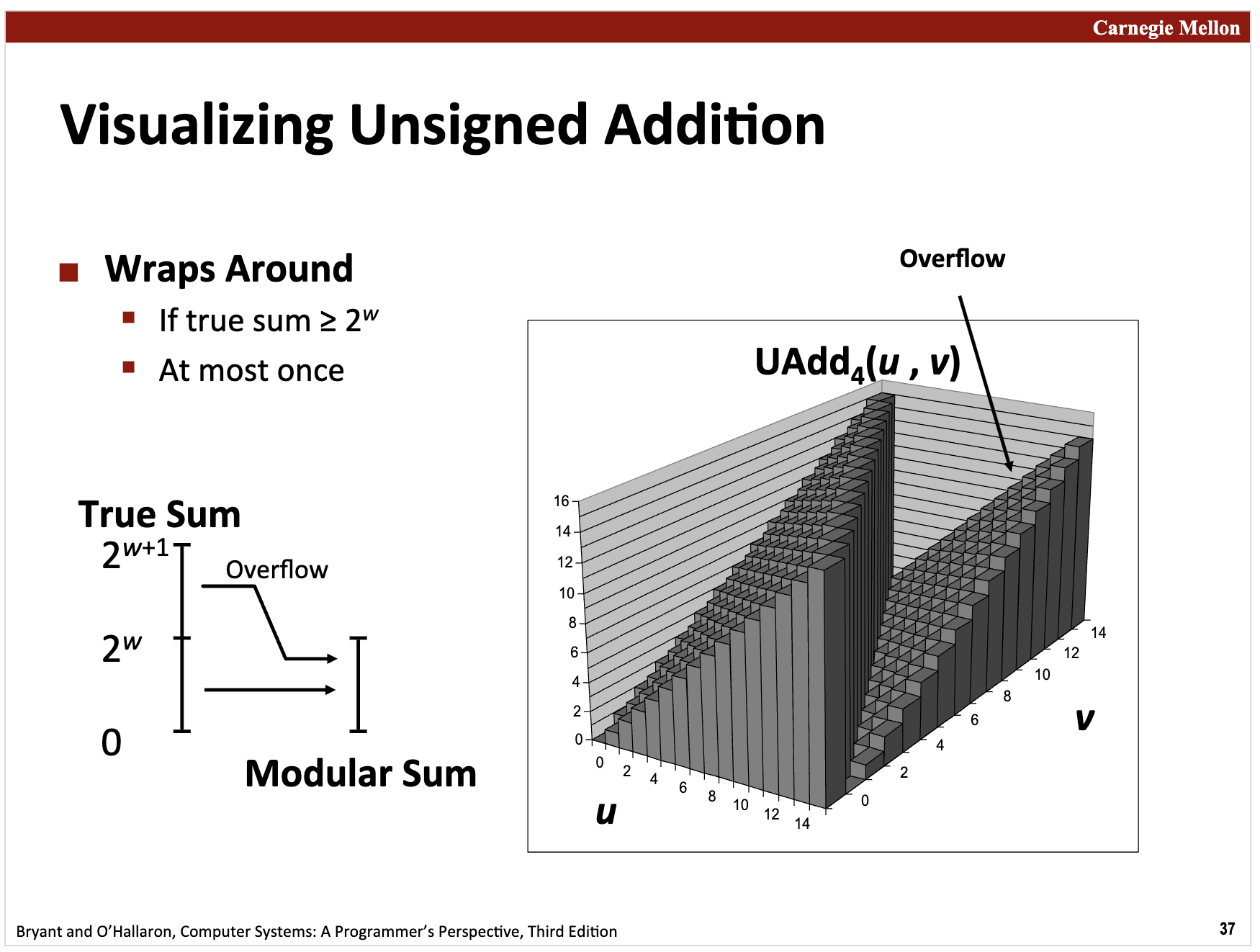
从上图可以看出
- 两个数的取值范围是 0 - 15
- 两数之和的取值范围是 0 - 15
- 当和为 16 时,掉到了 0
- 当和为 30 时,掉到 14,例如:14+16 取模后值为 14
- 当和为 31 时,掉到 15,例如:15+16 取模后值为 15
- 当和为 312 时,掉到 0,例如:16+16 取模后值为 0
补码加法

两个补码的加法,看起来像是普通的加法。意味着想要减去一个数,可以加上它的负数。
不溢出
| bit(补码) | 值 | |
|---|---|---|
| 加数 1 | 1101 | -3 |
| 加数 2 | 0101 | 5 |
| 和 (不忽略进位) | 10010 | 18 |
| 和 (忽略进位) | 0010 | 2 |
结论:期望值是 2,最后的结果是 2
| bit(补码) | 值 | |
|---|---|---|
| 加数 1 | 1011 | -5 |
| 加数 2 | 0011 | 3 |
| 和 (不忽略进位) | 1110 | -2 |
| 和 (忽略进位) | 0111 | -2 |
结论:期望值是 -2,最后的结果是 -2
负溢出
| bit(补码) | 值 | |
|---|---|---|
| 加数 1 | 1101 | -3 |
| 加数 2 | 1010 | -6 |
| 和 (不忽略进位) | 10111 | 18 |
| 和 (忽略进位) | 0111 | 7 |
期望值是 -9,最后的结果是 7
重点
两个负数相加,得到了正数,称为负溢出
正溢出
| bit | 值 | |
|---|---|---|
| 加数 1 | 0111 | 7 |
| 加数 2 | 0101 | 5 |
| 和 (不忽略进位) | 1100 | -4 |
| 和 (忽略进位) | 0111 | -4 |
重点
两个正数相加,得到了负数,称为正溢出